Theoretical peak patterns

Predicting elemental XRF (X-Ray Fluorescence) spectra

In order to unravel measured x-ray fluorescence (XRF) spectra it is essential to be able to compute the theoretical spectral emission patterns for individual elements. An XRF spectrum consists of a number of peaks whose positions/energies (expressed in kilo electron Volt) are specific for a given element. To a first approximation the intensities of the peaks are proportional the concentration of the element. However if we look with more scrutiny it turns out that the exact height proportions of the peaks varies with the thickness of the sample. Let’s skip the theoretical background and simply plot such an XRF spectrum. For now, simply import ElementXRF() and instantiate it for lead (Pb).

If you are interested in the physics behind this, you can find the gory details in a later section…

from moseley import ElementXRF
import matplotlib.pyplot as plt

Plotting a theoretical X-ray fluorescence spectrum can be done with the .plot_spectrum() method.

# initialize plot 
fig, axs = plt.subplots(ncols=4, figsize=[15, 4], sharex=True, sharey=False)
axs = axs.flatten()

# iterate over a list of different sample thicknesses 
for h_mm, ax in zip([0.001, 0.01, 0.1, 0.5], axs):   
    Pb_xrf = ElementXRF('Pb', h_mm=h_mm) 
    Pb_xrf.plot_spectrum(facecolor='k', ax=ax, xlim=[1, 17], vlines_colors='r') 
    ax.set_title(f'Pb (h={h_mm}mm)')  
    ax.set_xlim(xmax=20)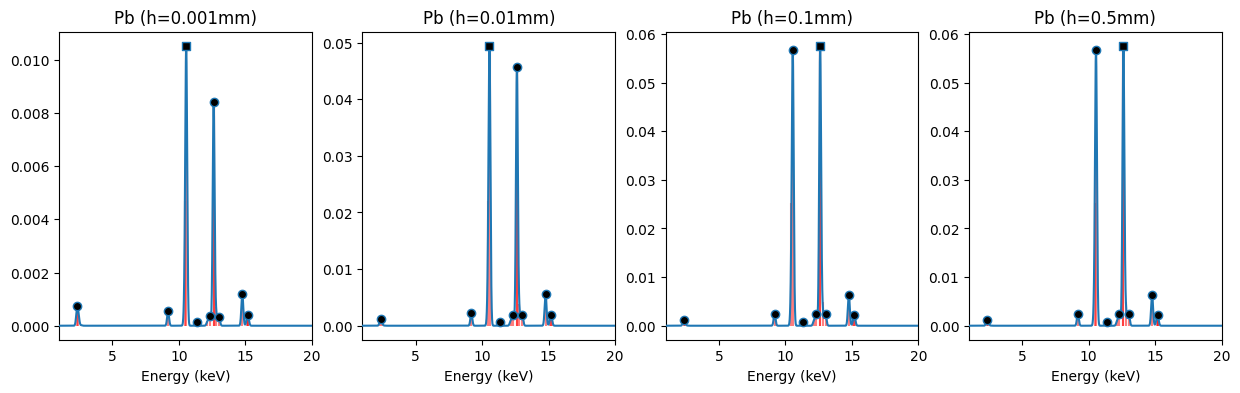

We can see here that these spectra (blue with black markers) for lead consist of multiple Gaussian shaped peaks. Most of these peaks are the result of closely spaced emission lines (red color). Each emission line corresponds to a specific transition of an electron between different electron shells. Although these patterns for lead samples of different thicknesses look fairly similar, their precise proportions vary.

If you want to inspect emission lines in detail you can take a look the .lines_table attribute.

Pb_xrf.lines_table # 0.5 mm
name label energy trans_prob fluo_yield jump_coeff attenuation intensity
0 Lb4 Pb_L1M2 12.3070 0.338604 0.112000 0.135060 0.462812 0.002371
1 Lb3 Pb_L1M3 12.7950 0.401364 0.112000 0.135060 0.487145 0.002958
2 Lg2 Pb_L1N2 15.0991 0.114773 0.112000 0.135060 0.378123 0.000656
3 Lg3 Pb_L1N3 15.2175 0.145259 0.112000 0.135060 0.310437 0.000682
4 Ln Pb_L2M1 11.3490 0.018116 0.373000 0.285714 0.412679 0.000797
5 Lb1 Pb_L2M4 12.6140 0.787801 0.373000 0.285714 0.478221 0.040150
6 Lg1 Pb_L2N4 14.7657 0.165149 0.373000 0.285714 0.364340 0.006412
7 Lg6 Pb_L2O4 15.1793 0.028934 0.373000 0.285714 0.381387 0.001176
8 Ll Pb_L3M1 9.1840 0.037951 0.360000 0.600958 0.292015 0.002398
9 La2 Pb_L3M4 10.4490 0.076339 0.360000 0.600958 0.363219 0.005999
10 La1 Pb_L3M5 10.5510 0.683544 0.360000 0.600958 0.368916 0.054556
11 Lb6 Pb_L3N1 12.1432 0.010655 0.360000 0.600958 0.454454 0.001048
12 Lb2,15 Pb_L3N4,5 12.6007 0.169784 0.360000 0.600958 0.477560 0.017542
13 Lb5 Pb_L3O4,5 13.0143 0.021727 0.360000 0.600958 0.497792 0.002340
14 Mg Pb_M3N5 2.6538 1.000000 0.005047 0.137090 0.027508 0.000019
15 Mb Pb_M4N6 2.4443 0.997068 0.031350 0.209486 0.074410 0.000487
16 Ma Pb_M5N6,7 2.3423 1.000000 0.030775 0.430848 0.068258 0.000905

FUNCTIONS

source

get_attenuation

 get_attenuation (element, emission_energy_keV,
                  excitation_energy_keV='rhodium_Ka', h_mm=0.1)

*Attenuation factors for emissions at emission_keVs for pure sample with thickness h_mm.

See Thomsen_2007 equation 11.

Returns: att_list (array of floats)*

source

plot_pattern

 plot_pattern (ptrn_dict, ax=None, offset=0, color=None)

Plot a single element peak pattern.

source

find_peaks

 find_peaks (x, y, min_prom=0.001)

*Find peaks in spectrum x, y with minimal prominence min_prom=

Returns: peaks_xy*

source

gaussian_convolve

 gaussian_convolve (peak_energies, peak_intensities, x_keVs=None,
                    std=0.01)

*Convolves line spectrum defined by peak_energies and peak_intensities

with a Gaussian peak shape.*

source

ElementXRF

 ElementXRF (element, excitation_energy_keV='rhodium_Ka', h_mm=0.1,
             x_keVs=None, std=0.01, min_prom=0.001)

Computes fluorescence emission line energies and intensities for element.

10/xraydb.material_mu('Pb', 22100)
np.float64(0.013224338571882998)
# https://xraypy.github.io/XrayDB/examples.html#mu-calculations-for-materials
mu_20kev = xraydb.material_mu('CaCO3', 20000, density=2.71)
print("CaCO3 1/e depth at 20keV = {:.3f} mm".format(10/mu_20kev))
CaCO3 1/e depth at 20keV = 0.648 mm
xraydb.chemparse('(PbCO3)2Pb(OH)2')
{'Pb': 3.0, 'C': 2.0, 'O': 8.0, 'H': 2.0}
lead_white = '(PbCO3)2Pb(OH)2'
mu_lead_white = xraydb.material_mu(lead_white, 22100,density=5)
10 * 1/mu_lead_white
np.float64(0.03733713607717201)
Pb_rho = xraydb.atomic_density('Pb') 
Pb_rho
11.34
mass_mu_emiss = xraydb.mu_elam('Pb', 22100)
mass_mu_emiss
np.float64(66.6826707720918)
element = 'Pb' 
density = 11.34 
energy = 22100 
emission_depth_um = 10000/(xraydb.mu_elam(element, energy) * density) 
emission_depth_um
np.float64(13.224338571882996)
10000 / xraydb.material_mu('Pb', energy, density=density)
np.float64(13.224338571882999)